Developing tools to uncover the collective dynamics hidden within noisy brain activity patterns
Closing remarks for the NSF CAREER award IIS-1845836
Originally published on Memming’s Substack
In 2018, while serving as a tenure-track assistant professor at Stony Brook University, the author submitted a research grant proposal to the National Science Foundation (NSF) aimed at uncovering the “algorithm” underlying brain activity. Drawing inspiration from cognitive algorithms, the research adopted a data-centric approach rather than starting from mathematical principles.
The methodology allowed measured neural activity to reveal underlying algorithms using the language of nonlinear dynamical systems—termed the “bottom-up approach.” Despite partial measurements capturing only a fraction of neurons in large network computations, the research assumed that sufficiently large population activity could reflect “the effective collective dynamics.”
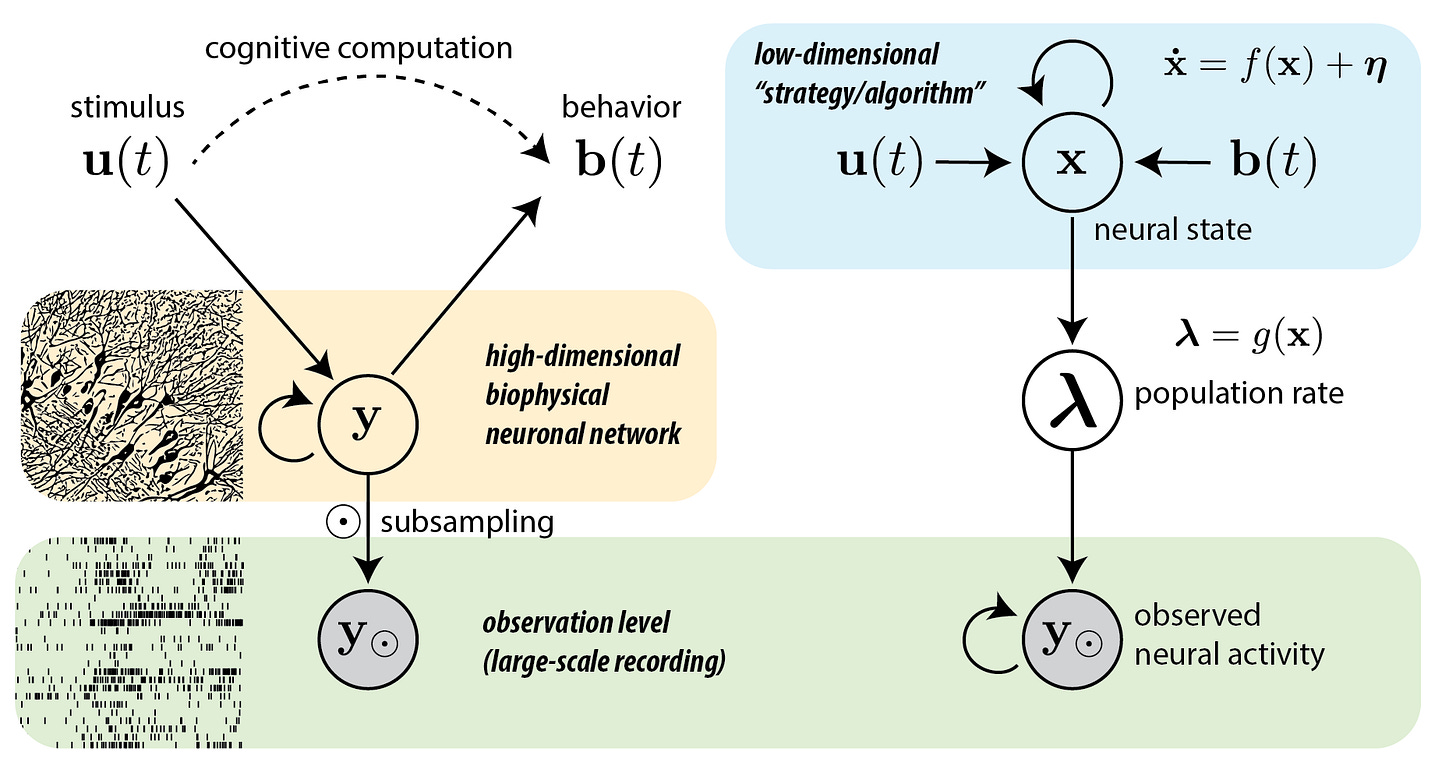
The proposal, titled “CAREER: Dynamical Systems Modeling of Large-Scale Neural Signals Underlying Cognition,” received funding in fall 2019 and concluded in 2023 after four years of research advancing mathematical and statistical neurotechnology.
Research Aims and Outcomes
Aim 1: Interpretable Modeling of Neural Time Series [1,2,3,4,6,7,8,11,15]
The research demonstrated that periodic and quasi-periodic attractors, beyond continuous attractors, can support learning arbitrarily long temporal relationships. Key findings included:
- Nonlinear oscillations ubiquitous in nervous systems offer advantages for training artificial recurrent neural networks—a significant result for neuro-AI development
- The widely-used Gaussian processes prior on neural trajectories equates to latent linear stochastic processes through the Hida-Matern connection, limiting their ability to mimic nonlinear attractor dynamics
- Practical statistical methods were developed for estimating time constants in spontaneous dynamics
- Improvements to autoregressive generalized linear models were achieved
- Research revealed lateralization in auditory cortex recurrent connectivity correlates with longer network time constants during inter-trial intervals
Aim 2: Real-time Model Fitting [9,10,12,13,14]
To enable next-generation experiments with real-time neural state-space perturbation and control, the research focused on accelerating inference for streaming neural recordings:
- Linear-time inference for Gaussian processes latent trajectory models was developed using the Hida-Matern connection
- Online approximate Bayesian filtering methods were improved by recognizing that practically all methods assume exponential family approximate posterior distributions
- These advances significantly enhanced inference quality and speed
Aim 3: Control Algorithm for Exploration of Brain States [5]
This aim targeted learning neural dynamics of disease attractor dynamics and developing novel methods to explore brain states for meta-stable states supporting normal function:
- An analog electronic circuit test platform exhibiting bistable dynamics with unknown control policies was built
- A novel control algorithm maximizing exploration was developed and tested
- Original plans to test the closed-loop system in traumatic brain injury coma patients faced unforeseen collaboration obstacles
- Future continuation is planned through RyvivyR and new collaborators
Publications and Research Output
The lab generated numerous manuscripts supported by this project:
-
Sokół, P., & Park, I. M. (2020). Information geometry of orthogonal initializations and training. International Conference on Learning Representations (ICLR).
-
Dowling, M., Zhao, Y., & Park, I. M. (2020). Non-parametric generalized linear model. arXiv [stat.ML] (revising).
-
Nassar, J., Sokol, P. A., Chung, S., Harris, K. D., & Park, I. M. (2020). On 1/n neural representation and robustness. Advances in Neural Information Processing Systems (NeurIPS).
-
Arribas, D. M., Zhao, Y., & Park, I. M. (2020). Rescuing neural spike train models from bad MLE. Advances in Neural Information Processing (NeurIPS).
-
Jordan, I. D., & Park, I. M. (2020). Birhythmic Analog Circuit Maze: A Nonlinear Neurostimulation Testbed. Entropy, 22(5), 537.
-
Dowling, M., Sokół, P., & Park, I. M. (2021). Hida-Matérn Kernel. arXiv [stat.ML] (revising).
-
Jordan, I. D., Sokół, P. A., & Park, I. M. (2021). Gated Recurrent Units Viewed Through the Lens of Continuous Time Dynamical Systems. Frontiers in Computational Neuroscience, 15, 67.
-
Neophytou, D., Arribas, D. M., Arora, T., Levy, R. B., Park, I. M., & Oviedo, H. V. (2022). Differences in temporal processing speeds between the right and left auditory cortex reflect the strength of recurrent synaptic connectivity. PLoS Biology, 20(10), e3001803.
-
Dowling, M., Zhao, Y., & Park, I. M. (2023). Real-time variational method for learning neural trajectory and its dynamics. International Conference on Learning Representations (ICLR).
-
Dowling, M., Zhao, Y., & Park, I. M. (2023). Linear Time GPs for Inferring Latent Trajectories from Neural Spike Trains. International Conference on Machine Learning (ICML).
-
Park, I. M., Ságodi, Á., & Sokół, P. A. (2023). Persistent learning signals and working memory without continuous attractors. arXiv [q-bio.NC] (revising).
-
Park, I. M. (2023). Fisher information of log-linear Poisson latent processes. (under review).
-
Dowling, M., Zhao, Y., & Park, I. M. (2023). Smoothing for exponential family dynamical systems. (under review).
-
Vermani, A., Park, I. M., Nassar, J. (2023). Leveraging generative models for unsupervised alignment of neural time series data. (under review).
-
Ságodi, Á., Sokół, P. A., & Park, I. M. (2023). RNNs with gracefully degrading continuous attractors. (under review).
Dissertations
-
Nassar, J. (2022). Bayesian Machine Learning for Analyzing and Controlling Neural Populations. PhD dissertation.
-
Jordan, I. (2022). Metastable Dynamics Underlying Neural Computation. PhD dissertation.
-
Sokół, P. (2023). Geometry of learning and representation in neural networks. PhD dissertation.
-
Dowling, M. (2023). Approximate Bayesian Inference for State-space Models of Neural Dynamics. PhD dissertation.